梯子图形的面积怎么求，梯子图形的面积怎么求公式

2用于直角三角形中的相关计算 3有利于你记住余弦定理，它是余弦定理的一种特殊情况中国最早的一部数学着作 周髀算经 的开头，记载着一段周公向商高请教数学知识的对话周公问“我听说您对数学非常精通，我想请教一下天没有梯子可以上去，地也没法用尺子去一段一段丈量，那么怎样才能；20170818 所有图形的周长面积的公式 45 20110201 所有图形的面积和周长的公式 251 20150412 总结所有图形面积体积周长公式 838 20090218 所有图形的周长和面积的公式 5354 20111009 各种图形的面积，周长计算公式 20070203 各种图形的面积·周长计算公式 164 20181117 求所有；”此为验算勾方股方的面积之和，与弦方的面积二十五相等从图形上来看，大正方形减去四个三角形面积后为弦方，再是 大正方形 减去 右上左下两个长方形面积后为 勾方股方之和因三角形为长方形面积的一半，可推出 四个三角形面积 等于 右上左下两个长方形面积，所以 勾方+股方=弦方注意；可能需要使用测量带或激光测距仪来确保精确度此外，对于高处的棱锥，可能还需要借助梯子或其他升高设备来方便地进行测量通过准确地应用这个公式，我们可以快速而准确地计算出棱锥的侧面积，这对于工程设计建筑施工等领域具有重要意义正确理解和应用这个公式，可以帮助我们更好地处理和解决实际问题；我们首先来推导梯形的面积公式设梯形的上底为a，下底为b，高为h我们可以将梯形分成一个矩形和两个三角形，如图所示根据几何知识，矩形的面积为a*h，两个三角形的面积分别为a+b*h2和ab*h2将这三部分的面积相加，即可得到整个梯形的面积化简公式后，我们可以得到梯形的面积公式；第一步树梯子这是最简陋一个图形如图1，也是最基本的一步图1 图2第二步做头尾上面的三部分，先分析开头和结尾部分，开头是什么呢？题中的已知可输入条件，也就是三条边的边长a，b，c结尾是什么呢？处理完成后的两个结果，即周长l和面积s图3 图4第三步连头尾如何将开头和结尾连接起来呢？也就是a；周公问quot我听说您对数学非常精通，我想请教一下天没有梯子可以上去，地也没法用尺子去一段 一段丈量，那么怎样才能得到关于天地得到数据呢？quot商高回答说quot数的产生来源于对方和圆这些形体的认识其中有一条原理当直角三角形#39矩#39得到的一条直角边#39勾#39等于3，另一条直角边#39股#39等于4的时候，那么它的。

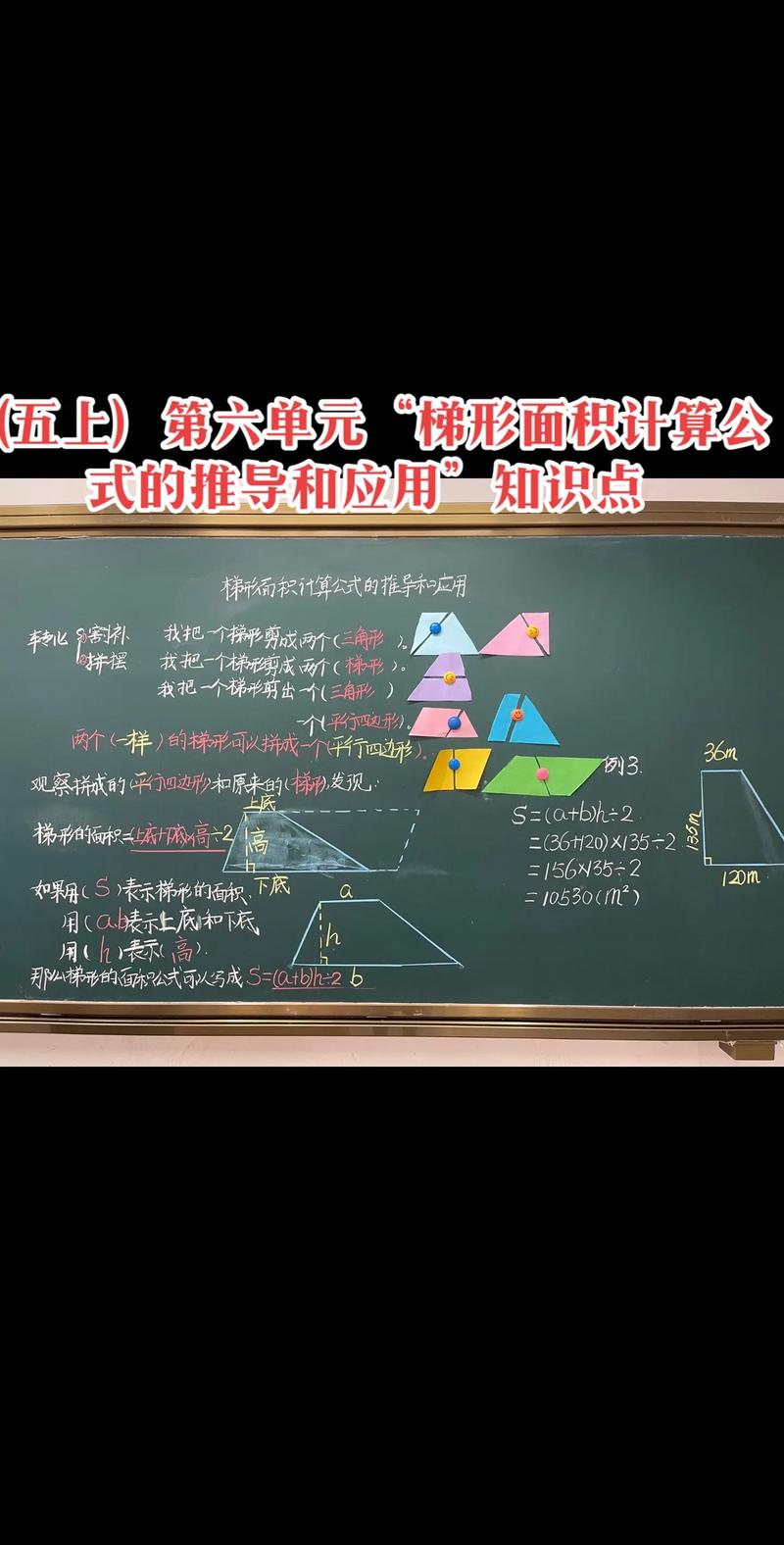
梯形的面积公式推导过程及其相关知识如下1假设梯形的上底为a，下底为b，高为h梯形的面积为5+10×6÷2=455+10×6÷2=45平方单位因此，梯形的面积公式为梯形面积=上底+下底×高÷22梯形具有两个相等的角，两个互补的角和两个对角线这种形状最早在古希腊数学家欧。

平行四边形的面积平行四边形的面积主要是指比乘高的面积，如果平行四边形的边长为a，高是h，可以直接套用公式，计算公式为S = ah计算的方法比较简单，只需要把数字放入到其中即可生活中比较常见的平行四边形有哪一些主要是窗户壁挂式电视晾衣架桌子瓷砖地板砖扇子推拉门梯子这些全部都；梯形的体积=上底+下底×高÷2×总长度梯形的体积计算公式是梯形的体积=上底+下底×高÷2×总长度平行的两边叫做梯形的底边，较长的一条底边叫下底，较短的一条底边叫上底，另外两边叫腰，夹在两底之间的垂线段叫梯形的高；在数学建模中，梯形可以用来表示各种不同的物理或抽象概念，如面积计算几何变换等体育用品跳高杆跳高杆的横截面有时可以近似看作是梯形，这种设计可能有助于增加杆的强度和稳定性电子元件某些电子元件的形状可能近似于梯形，这种设计可能是为了满足特定的电气性能或安装需求这些只是梯形可以联想。

66菱形面积=对角线乘积的一半，即S=a×b÷2 67菱形判定定理1 四边都相等的四边形是菱形 68菱形判定定理2 对角线互相垂直的平行四边形是菱形 69正方形性质定理1 正方形的四个角都是直角，四条边都相等 70正方形性质定理2正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角 71；梯形的面积计算公式是基于其底边长度和高具体而言，梯形的面积可以通过以下公式计算面积 = 上底 + 下底 * 高 2这个公式不仅适用于等腰梯形和直角梯形，同样适用于所有类型的梯形了解这个公式对于解决与梯形面积相关的数学问题非常有用在几何学中，梯形的性质和定理也是研究的重点例如；根据海伦公式求已知三角形的三边分别是abc，求面积先算出周长的一半p=12a+b+c，然后根据公式，代入数值即可；如怎样证明勾股定理？学生通过自学，中等以上的学生基本掌握，这时能激发学生的表现欲2教师引导学生按照要求进行拼图，观察并分析 1这两个图形有什么特点？2你能写出这两个图形的面积吗？ 3如何运用勾股定理？是否还有其他形式？ 这时教师组织学生分组讨论，调动全体学生的积极性，达到人人参与的效果，接着全班。

将图形转化为边在格线上的图形，以便于计算图形面积，体现了数形结合的思想学生会想到用quot数格子quot的方法，这种方法虽然简单易行，但对于下一步探索一般直角三角形并不适用，具有局限性因此教师应引导学生利用quot割quot和quot补quot的方法求正方形C的面积，为下一步探索复杂图形的面积做铺垫 突破等腰直角三角形的束缚，探索。